1st Oct, 2023 | Rinkal J.
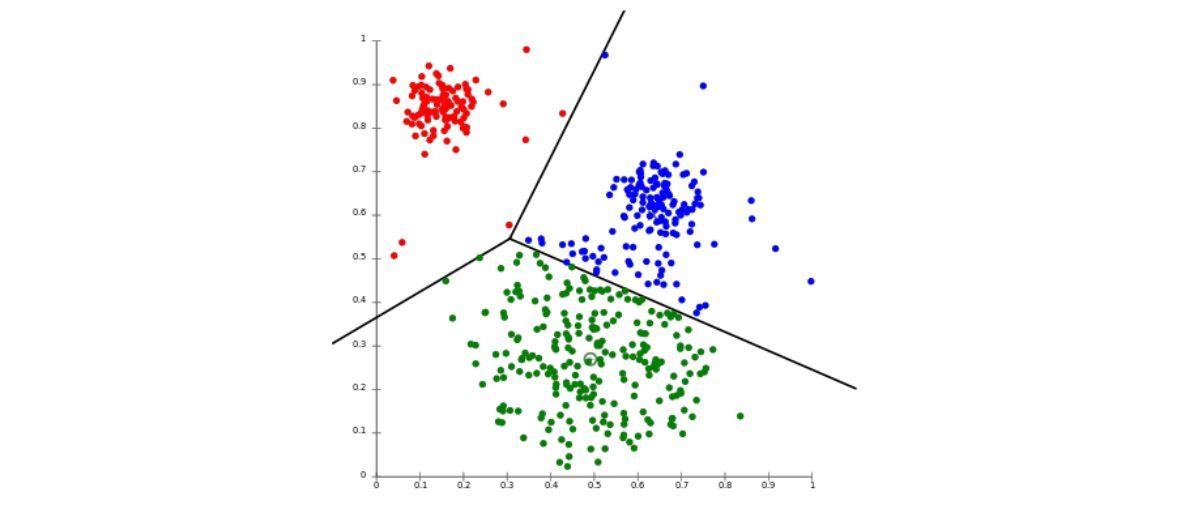
In the field of machine learning, one of the key objectives is to achieve accurate predictions. These predictions can be achieved through various learning algorithms, categorized as supervised and unsupervised.
K-means clustering is one such unsupervised algorithm that groups data points based on their similarity. In this blog, we will explore the use cases, advantages, and working principles of the K-means clustering algorithm.
K-means clustering is an unsupervised machine learning approach that uses similarities to divide a dataset into K different clusters. The algorithm aims to minimize the within-cluster variance, ensuring that data points within the same cluster are as similar as possible while data points in different clusters are as dissimilar as possible.
Source: K-means clustering
The K-means clustering algorithm has gained remarkable popularity in the field of machine learning and data analysis due to several compelling reasons. Its simplicity, versatility, and effectiveness in solving a wide array of problems have positioned it as a staple tool in the data scientist's toolkit.
Let's delve into the reasons behind the widespread popularity of the K-means algorithm:
The K-means algorithm's straightforward concept and implementation are major contributors to its popularity. Its simplicity lies in the intuitive idea of grouping data points into clusters based on their similarity. This accessibility makes it an excellent starting point for newcomers to machine learning.
K-means is known for its computational efficiency, making it suitable for handling large datasets. Its time complexity is relatively low, allowing it to process data quickly and efficiently. This speed is particularly advantageous in scenarios where real-time or near-real-time analysis is crucial.
As an unsupervised learning algorithm, K-means doesn't require labeled data for training. It autonomously discovers patterns and structures within data, making it valuable for exploratory data analysis and uncovering hidden insights.
The K-means algorithm's versatility is a key reason behind its widespread adoption. It can be applied to various domains, including customer segmentation, image compression, natural language processing, and more. Its adaptability makes it a valuable tool for data scientists working in diverse fields.
K-means produces clusters that are relatively easy to interpret. Each cluster represents a group of similar data points, allowing analysts to derive meaningful insights from the results. This interpretability is essential for making informed decisions based on the clustering outcomes.
In an era of big data, K-means' ability to handle large datasets efficiently is a significant advantage. Its performance scales well as the volume of data increases without placing undue strain on computational resources.
K-means often serves as a baseline or benchmark for evaluating the performance of more complex clustering algorithms. Its simplicity and widespread familiarity allow researchers and practitioners to gauge the efficacy of advanced techniques by comparing them against K-means results.
While determining the optimal number of clusters ('k') can be a challenge, K-means provides the flexibility to experiment with different values of 'k'. With techniques like the elbow method or silhouette score, data analysts can make informed decisions about the appropriate number of clusters.
The K-means algorithm's success stories in various practical applications have contributed to its popularity. It has proven its value in enhancing marketing strategies, image compression techniques, anomaly detection in cybersecurity, healthcare data analysis, and more.
Let's use an example to see how K-means works step by step. The algorithm can be divided into around 5 to 6 main steps.
Choose the desired number of clusters (K) that you want the algorithm to identify within your dataset.
Randomly assign K cluster centroids to your dataset. These centroids serve as the starting points for each cluster.
For each data point in your dataset, calculate the distance between that point and each cluster centroid using a distance metric (commonly the Euclidean distance). Place the data point to the cluster with the closest centroid.
Once all data points have been assigned to clusters, calculate the new centroids for each cluster by taking the mean (average) of all the data points belonging to that cluster.
Steps 3 and 4 should be repeated until convergence occurs, which occurs when the cluster assignments no longer change appreciably or when the maximum number of iterations is reached.
The final output of the K-means clustering algorithm is a set of K clusters with each data point assigned to one of these clusters.
Source: K-means
Choosing the correct number of clusters (K) is crucial for effective clustering. Selecting too few or too many clusters can lead to inaccurate or meaningless results. There are various methods to determine the optimal value of K, such as the "elbow method" or silhouette analysis, which help identify the point of diminishing returns for increasing the number of clusters.
The K-means algorithm, a cornerstone of unsupervised machine learning, has gotten a lot of attention for its ability to find patterns in data. K-means, which groups comparable data points into clusters, has made its way into a wide range of practical applications.
One of the most prevalent applications of K-means is in customer segmentation. Businesses can categorize their customers into distinct groups based on purchasing behavior, preferences, and demographics. This segmentation enables tailored marketing strategies, personalized product recommendations, and more effective targeting, ultimately leading to increased customer satisfaction and higher conversion rates.
In the field of image processing, K-means is essential for picture compression. The technique minimises image data size by grouping related colours together and expressing them with a limited palette. This compression is especially effective for web graphics and apps that require quick loading times and efficient storage.
Detecting anomalies in vast datasets is a crucial task in cybersecurity. K-means aids in this endeavor by establishing clusters of normal patterns and identifying deviations from these patterns. By flagging these anomalies, security teams can proactively address potential threats and vulnerabilities, bolstering the overall security posture.
Healthcare generates an enormous amount of patient data, which can be challenging to manage effectively. K-means assists healthcare professionals in segmenting patient populations based on medical history, risk factors, and treatment responses. These clusters facilitate personalized treatment plans, disease prediction, and optimized allocation of medical resources.
The algorithm's clustering capabilities are leveraged in recommendation systems across online platforms. By grouping users with similar preferences, K-means enables platforms to suggest products, services, or content based on the preferences of similar users.
K-means also finds a place in the realm of Natural Language Processing (NLP). It can cluster similar documents, sentences, or even words in text data. This is valuable for tasks such as summarization, topic modeling, and sentiment analysis, making it easier to extract meaningful insights from large volumes of textual information.
In each of these use cases, the K-means algorithm demonstrates its adaptability and utility, showcasing its capacity to uncover patterns, enhance decision-making, and streamline processes across a diverse range of fields.
The K-means algorithm has a number of benefits that have contributed to its broad appeal. It does, however, have certain restrictions. Let's look at the advantages and disadvantages of the K-means algorithm.
The K-means algorithm's simplicity is a major advantage. Its straightforward concept of partitioning data into clusters based on similarity makes it easy to understand and implement. This accessibility is especially valuable for newcomers to the field of machine learning.
K-means is known for its computational efficiency, making it suitable for handling large datasets. Its complexity is relatively low, allowing it to process data quickly and efficiently. This speed is advantageous for real-time or near-real-time applications.
The algorithm's efficiency scales well with the increase in the number of data points. This scalability makes K-means applicable to datasets of varying sizes, from small to large.
K-means operates under the unsupervised learning paradigm, requiring no labeled data for training. It autonomously discovers patterns within data, making it valuable for exploratory data analysis and uncovering hidden insights.
The choice of the number of clusters, 'k,' is flexible. While determining the optimal 'k' can be challenging, various techniques like the elbow method or silhouette score can help data analysts make informed decisions about the appropriate number of clusters.
K-means produces clusters that are relatively easy to interpret. Each cluster represents a distinct group of data points with similar characteristics, aiding in deriving meaningful insights from the results.
K-means' convergence to a solution is sensitive to the initial placement of cluster centroids. Different initial placements can result in different final clusterings. Techniques like the k-means++ initialization method help mitigate this issue.
K-means assumes that clusters are of equal sizes and have spherical shapes. This assumption can lead to suboptimal results when dealing with clusters of varying sizes or non-spherical shapes.
The algorithm's performance heavily depends on the correct choice of the number of clusters ('k'). Incorrect 'k' values can lead to clusters that are not meaningful or informative.
K-means is sensitive to outliers, which can skew the placement of cluster centroids and affect the overall clustering results.
K-means assumes that clusters are separated by linear boundaries. It may not perform well on datasets with complex or non-linear cluster structures.
K-means clustering is a powerful technique for data analysis and pattern recognition. We can obtain insights and make informed judgements by grouping comparable data pieces together. K-means clustering has proven to be a beneficial tool in a variety of disciplines, including consumer segmentation, image compression, and genetic research.
Data analysts and machine learning practitioners can use K-means clustering to identify hidden patterns and extract useful information from their datasets by knowing the principles of the method and its applications.
Remember that K-means clustering is simply one of several available clustering methods, and its efficacy is dependent on the nature of the data and the situation at hand. Experimenting with various clustering algorithms can result in more accurate and insightful results.
Get insights on the latest trends in technology and industry, delivered straight to your inbox.
